Second-order Greeks are particularly useful for modeling stress scenarios.
In this article we explore the less common or unusual Greeks, of which there are many. We will extend our discussion up to third order Greeks, recognising that each Greek represents a specific partial derivative.
The Structured Products Risk Business Intelligence (RBI) from the SRP Greeks platform addresses not only the classic Greeks but also several rarer sensitivities, including DivSens, Charm and Vanna.
In this article, we will examine DivSens and Vanna in greater detail and illustrate some of their practical applications.
Let’s start with an extended overview table of the Greeks / sensitivities.
| N° | Greek | What it means | Order | Usual | Currently available on the platform |
| 1 | Delta (Δ) | Change in derivative price / Change in underlying price | First | Yes | Yes |
| 2 | Gamma (Γ) | Change in derivative Delta / Change in underlying price | Second | Yes | Yes |
| 3 | Vega (𝓥) or Kappa | Change in option price / Change in volatility (of the underlying) | First | Yes | Yes |
| 4 | Rho (ρ) | Change in option price / Change in risk-free interest rate | First | Yes | Yes |
| 5 | Theta (Θ) or Tau (τ) | Change in option price / Change in time (time decay) | First | Yes | Yes |
| 6 | DivSens or Epsilon | Change in option price / Change in the dividend yield of the underlying asset | First | No | Yes |
| 7 | Charm or Delta decay | Change in Delta / Change in time. For calculations, the platform uses a 1-business-day horizon | Second | No | Yes |
| 8 | Vanna | Change in Delta / Change in volatility or change in Vega / Change in underlying price. The two values are mathematically identical as Vanna is the second partial derivative of the option price with respect to the underlying price and the volatility | Second | No | Yes |
| 9 | Veta | Change in Vega / Change in time | Second | No | No |
| 10 | Vomma or Volga | Change in Vega / Change in volatility | Second | No | No |
| 11 | Color | Change in Gamma / Change in time | Third | No | No |
| 12 | Parmicharma | Change in Charm / Change in time | Third | No | No |
| 13 | Speed | Change in Gamma / Change in underlying price | Third | No | No |
| 14 | Ultima | Change in Vomma / Change in volatility | Third | No | No |
| 15 | Zomma | Change in Gamma / change in Volatility | Third | No | No |
| 16 | Elasticity or Omega | Percentage change option price / Percentage change in underlying price | No | No |
Source: Patrick Oberhaensli
Second-order Greeks are particularly useful for modeling stress scenarios, as they measure how quickly the primary Greeks (Delta and Vega) change in response to sharp movements in the underlying's price or its volatility.
Although Gamma (the second derivative of option price, relative to the underlying price) is widely (the most) recognised, other second-order Greeks can provide critical insights. For instance, Vanna describes the joint sensitivity to changes in both the underlying price and its volatility (we talk about “cross-partial derivatives”), while Vomma captures the variability of Vega itself.
Let's examine the less common Greeks - specifically Dividend Sensitivity / DivSens (Epsilon) and Vanna - in the context of globally aggregated S&P 500 structured products, focusing on the largest instruments in the market.
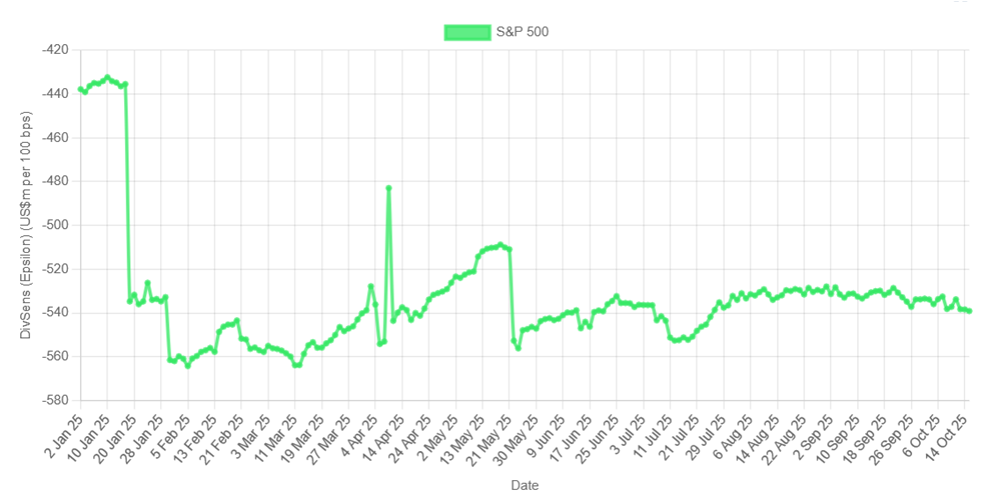
The graph below shows the current Epsilon development for the biggest S&P 500 structured products that are part of the SRP Greeks platform: the very high loss of about US$540 million for an increase of one percent in the dividend yield indicates the actual dominance of (Barrier) Reverse Convertible which exhibit negative Epsilon reflecting their short-put exposure (the Position Delta being positive).
Source: SRP Greeks
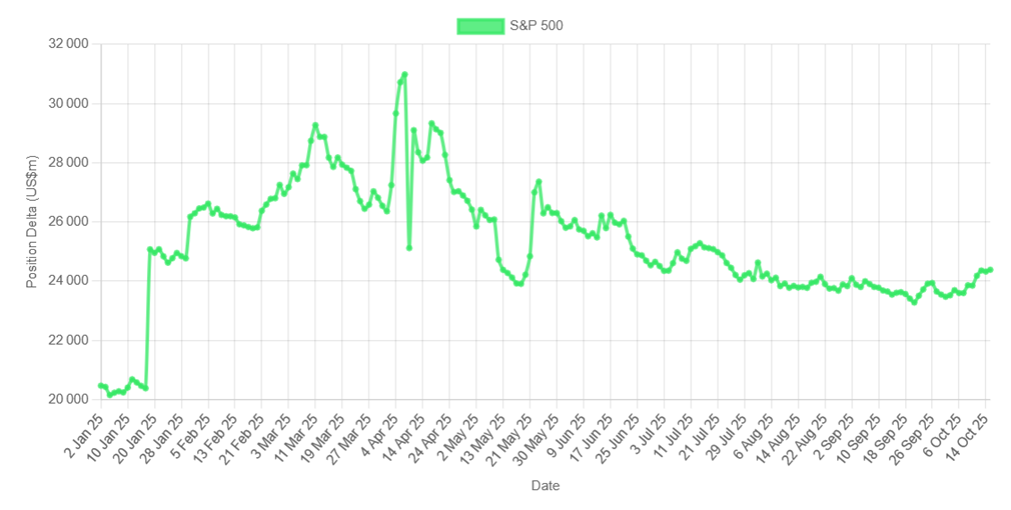
The corresponding positive Position Delta:
Source: SRP Greeks
From the standpoint of an investor, a high dividend yield at issuance is advantageous when creating a Reverse Convertible, as the embedded put option (which the investor sells) increases in value, allowing for a higher coupon on the product.
However, if the dividend yield rises after issuance, this becomes a disadvantage (losses are generated). For the hedger, it looks good as long as the dividend yield increase has been factored in: since the beginning of the year 2025 the exposure has clearly increased.
The graph below shows the current Vanna development for the biggest S&P 500 structured products that are part of the SRP Greeks platform.
Source: SRP Greeks
Vanna allows to estimate the significant increase in Position Delta (the graph above) that would be caused by a shock in volatility: as it happened during the 'Liberation Day' period early this April.
Historically, implied volatility (as indicated by the VIX index) has occasionally reached closing levels above 80% (annualised). When Position Delta is already high and then further amplified by a sudden and sharp volatility surge, a downside climax may occur, often presenting a tactical opportunity to go long.
April 2025 reflected that situation. For a Delta-neutral hedger, the Vanna effect can make re-hedging particularly challenging - the unwanted directional exposure to be corrected, especially in a market with large aggregate exposures - such as the structured products market, which in this analysis is taken as representative.
While Vanna is a second-order Greek, it becomes an essential, first-order risk when trading volatility instruments directly.
In the next article, we will return to the topic of volatility to explore its further practical implications and advanced applications—among them, the well-known phenomenon of the volatility smile, a key concept in understanding how to deal with weaknesses in standard pricing models.
Understanding and modeling this phenomenon are essential for accurate option pricing, risk management and developing more robust trading strategies in real markets.
Image: Neurobite/Adobe Stock
| This article is based on data and analysis provided by the SRP Greeks product. Find out more about SRP Greeks here |
Disclaimer
- This content is not intended as a solicitation or an offer; it is provided solely for informational purposes to professional investors
- The information presented herein has been prepared with great care; however, errors may still occur